Density-functional theory (DFT) is an exact alternative formulation of quantum mechanics, in which it is possible to calculate the total energy, the spin, and the charge density of many-electron systems in the ground state. In practice, it is necessary to use uncontrolled approximations that can mainly be verified against experimental data. Atoms and ions are simple systems, where the approximations of DFT can be easily tested. We have calculated within DFT the total energies, spin, and higher ionization energies of all the ions of elements with 1⩽Z⩽29. We find the calculations in close agreement with experiment, with an error of typically less than ca. 1% for 1⩽Z⩽29. Surprisingly, the error depends on the electronic configuration of the ion in both local spin density approximation and Perdew-Burke-Ernzerhof general gradient approximation and independent of both self-interaction correction and relativistic corrections. Larger errors are found for systems in which the spin-spin correlation is significant, which indicates the possible benefit from an orbital-dependent formulation of the correlation energy functional.
In the exact Kohn-Sham density-functional theory, the total energy versus the number of electrons is a series of linear segments between integer points. However, commonly used approximate density functionals produce total energies that do not exhibit this piecewise-linear behavior. As a result, the ionization potential theorem, equating the highest occupied eigenvalue with the ionization potential, is grossly disobeyed. Here, we show that, contrary to conventional wisdom, most of the required piecewise linearity of an arbitrary approximate density functional can be restored by careful consideration of the ensemble generalization of density-functional theory. Furthermore, the resulting formulation introduces the desired derivative discontinuity to any approximate exchange-correlation functional, even one that is explicitly density dependent. This opens the door to calculations of the ionization potential and electron affinity, even without explicit electron removal or addition. All these advances are achieved while neither introducing empiricism nor changing the underlying functional form. The power of the approach is demonstrated on benchmark systems using the local density approximation as an illustrative example.








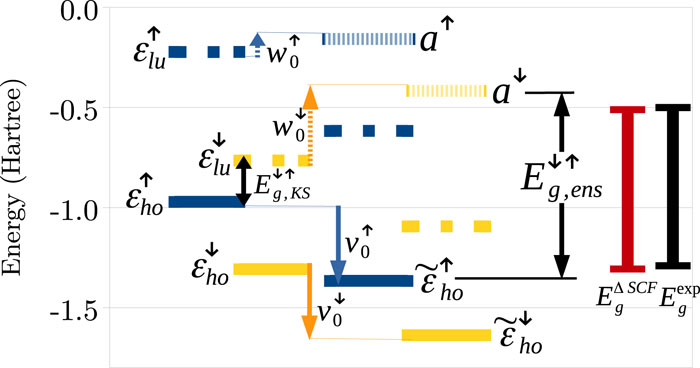
















 There are several approximations to the exchange-correlation functional in density-functional theory, which accurately predict total energy-related properties of many-electron systems, such as binding energies, bond lengths, and crystal structures. Other approximations are designed to describe potential-related processes, such as charge transfer and photoemission. However, the development of a functional which can serve the two purposes simultaneously is a long-standing challenge. Trying to address it, we employ in the current work the ensemble generalization procedure proposed by Kraisler and Kronik [Phys. Rev. Lett. 110, 126403 (2013)]. Focusing on the prediction of the ionization potential via the highest occupied Kohn-Sham eigenvalue, we examine a variety of exchange-correlation approximations: the local spin-density approximation, semi-local generalized gradient approximations, and global and local hybrid functionals. Results for a test set of 26 diatomic molecules and single atoms are presented. We find that the aforementioned ensemble generalization systematically improves the prediction of the ionization potential, for various systems and exchange-correlation functionals, without compromising the accuracy of total energy-related properties. We specifically examine hybrid functionals. These depend on a parameter controlling the ratio of semi-local to non-local functional components. The ionization potential obtained with ensemble-generalized functionals is found to depend only weakly on the parameter value, contrary to common experience with non-generalized hybrids, thus eliminating one aspect of the so-called “parameter dilemma” of hybrid functionals.
There are several approximations to the exchange-correlation functional in density-functional theory, which accurately predict total energy-related properties of many-electron systems, such as binding energies, bond lengths, and crystal structures. Other approximations are designed to describe potential-related processes, such as charge transfer and photoemission. However, the development of a functional which can serve the two purposes simultaneously is a long-standing challenge. Trying to address it, we employ in the current work the ensemble generalization procedure proposed by Kraisler and Kronik [Phys. Rev. Lett. 110, 126403 (2013)]. Focusing on the prediction of the ionization potential via the highest occupied Kohn-Sham eigenvalue, we examine a variety of exchange-correlation approximations: the local spin-density approximation, semi-local generalized gradient approximations, and global and local hybrid functionals. Results for a test set of 26 diatomic molecules and single atoms are presented. We find that the aforementioned ensemble generalization systematically improves the prediction of the ionization potential, for various systems and exchange-correlation functionals, without compromising the accuracy of total energy-related properties. We specifically examine hybrid functionals. These depend on a parameter controlling the ratio of semi-local to non-local functional components. The ionization potential obtained with ensemble-generalized functionals is found to depend only weakly on the parameter value, contrary to common experience with non-generalized hybrids, thus eliminating one aspect of the so-called “parameter dilemma” of hybrid functionals.



