Citation:

Abstract:
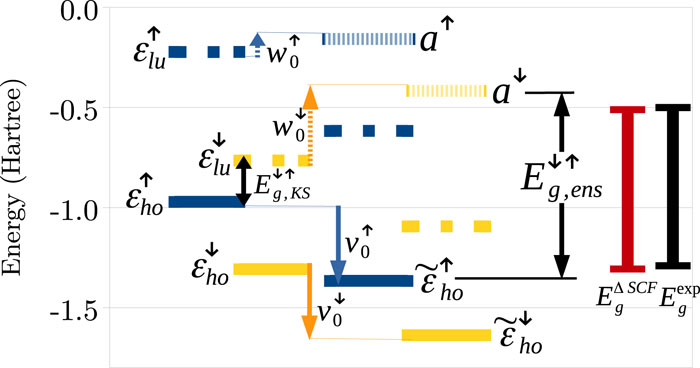
Calculations in Kohn–Sham density functional theory crucially rely on high-quality approximations for the exchange-correlation (xc) functional. Standard local and semi-local approximations fail to predict the ionization potential (IP) and the fundamental gap, departing from the Kohn–Sham orbital energies, due to the deviation of the total energy from piecewise-linearity and the absence of the derivative discontinuity. The ensemble generalization procedure introduced in Phys. Rev. Lett. 110, 126403 (2013) restores, to a large extent, these features in any approximate xc functional and improves its ability to predict the IP and the fundamental gap with negligible additional computational effort. In this work we perform an extensive study of atoms and first ions across the Periodic Table, generalizing the local spin-density and the Perdew–Burke–Ernzerhof approximations. By applying the ensemble generalization to a variety of systems, with s-, p-, and d-character, we assess the accuracy of the method and identify important trends. In particular, we find that the accuracy of our approach heavily depends on the character of the frontier orbitals: when d-orbitals are involved, the performance is far less accurate. Possible sources of error are discussed and ways for further improvement are outlined.




